重量级构造题
CF
qwq
## 1896G给定长度为 的排列 ,每次你可以询问 (要求元素互不相同),交互库返回这里面哪个位置最大。
次询问之后你需要找出 这些数的下标。
题解
赛时没写完,急急急。
把数分成 组,初始每组 个数,并且对于每组记录一下这组哪个位置最大, 次询问。
每轮求出最大的位置是哪个,只要在每组的最大位置里面询问一次就行。
接下来我们得从某一组里面删掉这个最大位置,现在这组不完整了,为了维护出这个结构,我们从其他组拉一些不是最大位置的元素到这组知道凑够 个数,再询问一次。这样可以发现确定答案的一个元素 个询问就够了。
当剩余元素 时候,再取出最大之后已经没有足够的元素组成一组了,这时候考虑一个性质:每组的最大值一定打赢过至少一场比赛,那么剩下的 个一定是最小的那几个,直接 次询问就能确定剩下 个最大值的排名。
The 2nd Universal Cup
qwq
R11
R10F
给你迷宫,有些地方不能走。bot 从起点走到终点,并且访问所有能走的地方至少一次。你需要发送命令给 bot(命令包括上下左右)。如果走过去的位置不能走就不走。你的命令必须是回文串。构造。无解输出 。
。
题解
赛时写对了。
连通就有解。
先从终点开始 dfs 一次整个迷宫回到自己,记录这个串为 。
那么我们试图构造答案为 ,其中 是回文。
现在转化为了已经访问每个点,只要从起点走到终点,把合法转移写出来 bfs 即可。
注意不能从起点开始 dfs,比如:
S111
1000
1T10
如果你开头放了 RRR 就没救了。
R10K
构造一个平面图, 个点,且度数 的点不超过四个。
题解
5:03 写对了,火大。
随便造。
一看就没救。
玩一下会发现 没救, 有救:
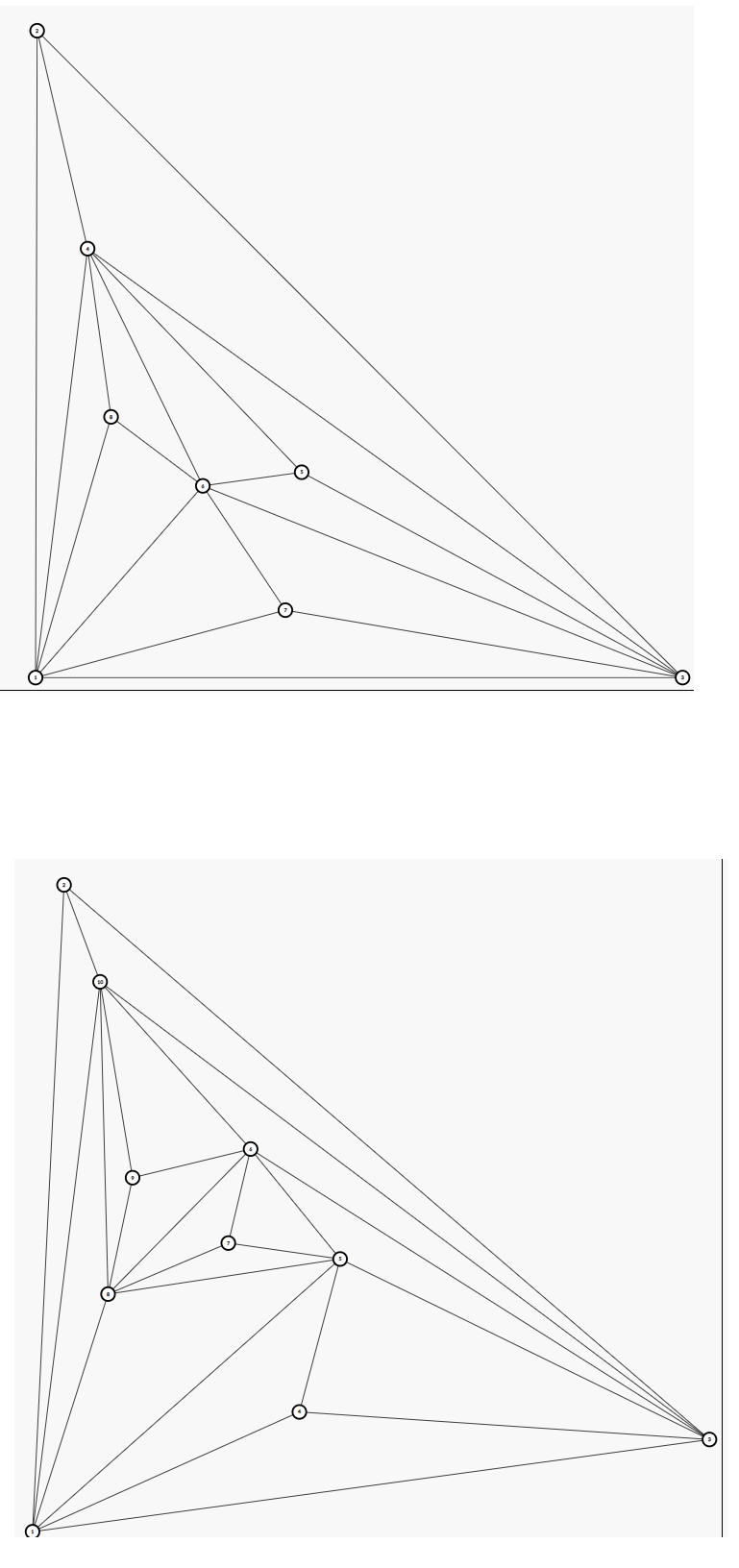
仔细一看:
这样就能加四个点,于是可以获得 的任意偶数的构造。
大力猜测奇数无解,过了。
R9K
构造 矩阵,值域 ,每个数出现不超过 次,相邻两个数 and 起来是 。
题解
这种题加点限制就行。
出现次数给他来个不超过 次, 把他紧到取 且大于等于 的最小 ,然后就是 。
考虑构造出第一行之后,后面可以:
00 11 02 13 04
11 22 13 24 10
20 31 22 33 24
31 42 33 44 30
40 01 42 03 44
这样整一下行列分别高低位。方便起见钦定 。
发现让 的第一行互不相同是不现实的,至少会有数出现两次。这样极端情况下矩阵出现次数最多的就是八次了,不太行。
但是你发现可以考虑一下奇偶性,如果两次出现位置奇偶性不同那就只会出现四次了。
一个简单的构造是类似回文的东西: 这样的。
直接搜就能搜出一个合法序列。
R8D
平面上有 个地铁站,一条地铁是一条折线,要求拐点都在整点处。
一条地铁不能自交,两条地铁只能在地铁站处相交。
现在第 个地铁站要求恰好 条线路经过。构造,并最小化地铁线路数量。
地铁站坐标 。
题解
赛时写挂了。
答案是 。
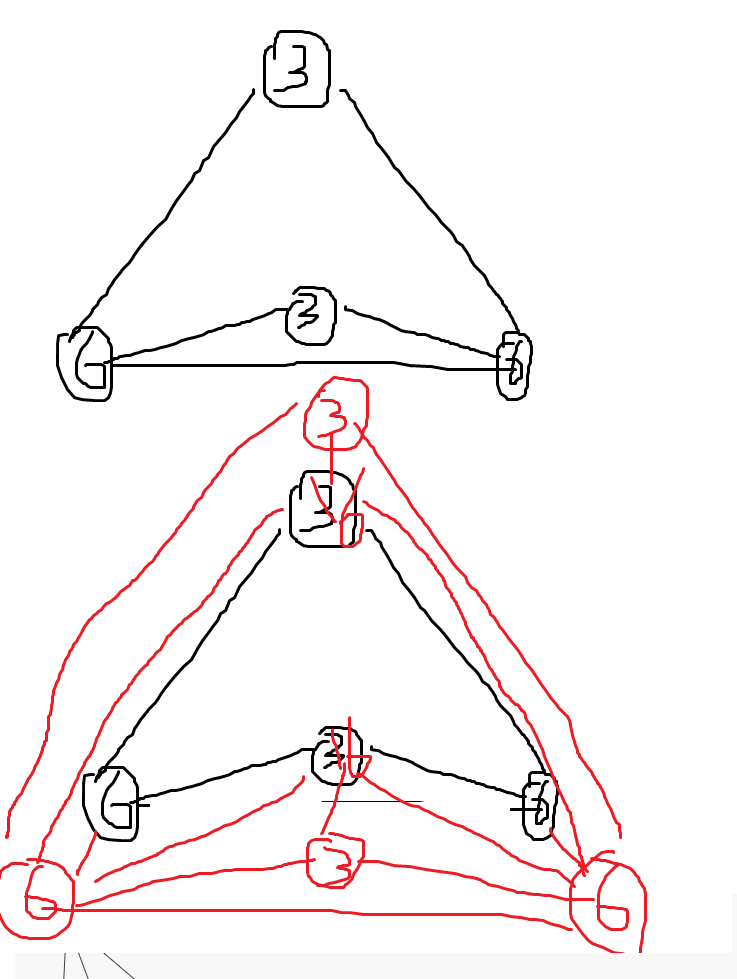
对于第 条线路,找到 的所有站建立 W 型线路。
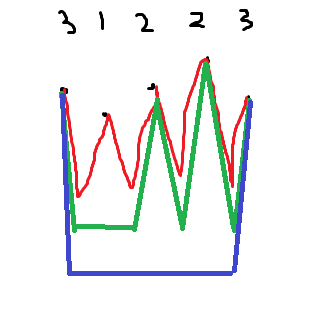
旋转一下坐标系就能保证这个做法一定成功。
qwq
R7L
通信,也放这得了。
给定序列 ,长度 ,值域 ull。Alice 读入 并发送一个长度不超过 的 ull 序列,测评库把这个序列的元素随机选择大端或者小端并发送给 Bob。Bob 得到测评库发来的序列,还原 。
题解
赛时写对了。
24\time 62 > 1000,我们可以给每个数记录一个信息。一个 ull 去掉两位信息位来判断有没有反转大小端( 位放 , 位放 )来记录 bit 信息。
一个数的信息可以看成:他大端读和小端读,他是大的那个还是小的那个。然后就好了。
qwq
R7F
构造二维平面无限平铺的 矩阵,每个 恰好三个邻居是 ,要求 占比 。
,你只要给出一个循环节。
题解
赛时写对了。
的 矩阵是合法的,这样可以构造 。
上界显然是 。因为每个十字至少有一个 。
考虑 的连通块:必须构成矩形,否则有 相邻两个 了。
我们试试只用宽度为 的矩形,题目可以转化为用
.111..
10001.
.111..
这样的图形铺满整个平面。
........-------
........|1.1.1|
......---.....---
......|1.0.0.0.1|
......---.....---
........|1.1.1|
........-------
..........|1.1.1|
........---.....---
........|1.0.0.0.1|
........---.....---
..........|1 1 1|
..........---------
............|1.1.1|
..........---.....---
..........|1.0.0.0.1|
..........---.....---
............|1 1 1|
............-------
注意到你可以这样子平铺,并且每一列的矩形长度你可以自己选定。
所以放一列 能带来 个 和 个 。
线性组合一下就能组合出 密度为 的解了。