VS 花花 (9-11)

输了。伤心。

隔壁链接

Problem 1：$\texttt\color{green}CF33E$

笨蛋模拟，纯练写代码。

Problem 2：$\texttt\color{green}CF842E$

树，加点，然后求多少个点可以作为直径的端点。

题解

其实这个题我还有点没想明白所以这个题解非常口胡我自己都看不下去。考虑所有直径的交，如果交至少有一条边那么答案的点分在它的两边，维护这两边的集合。

加入点时至少一个点集不会删掉，先看加入之后直径会不会长，如果不会可以按照上面丢进一个集合内。

如果变长了，加入对应集合，另一个集合不变；然后这个集合里可能仍然有能作为直径的点，遍历一次，如果可以就加入另一个集合，否则删除。

然后这个直径交点单点的时候可以通过上面的实现直接解决掉，但是我也不知道为什么。。看上去很有道理

Problem 3：$\texttt\color{green}CF1528E$

数 dag：

1. 每个点度数 $\le 3$；
2. 最长路径长度 $n$；
3. 建立新图，如果原图 $i\to j$ 有路径则加入 $(i,j)$ 的无向边，新图任意两点最短路 $\le 2$。

题解

答案三种情况：内向树，外向树，内向树和外向树公用一个根拼起来。

dp 是简单的。

Problem 4：$\texttt\color{red}CF1477D$

题意：无向图，定向，找两个拓扑序，对应位置不同的数量最大化。

题解

度数满的点位置一定相同，可以直接删掉。剩下的答案是能构造满的，只要把补图分解成若干至少两个点菊花。这个是简单的。

Problem 5：$\texttt\color{red}CF480E$

题意：01 矩阵，每次把一个点变成 $0$，然后求最大 $1$ 正方形的边长。

数据范围全是 $2000$。

题解

时光倒流，然后答案一定一直增。先求出倒流后最初的答案，维护每个点能往上走几个和往下走几个。

当加入一个点的时候，先修改这一列上的这些值，然后试着增加答案。

因为如果答案增加那么一定包含了修改的这个点，所以直接枚举这个点往左走几个，看到对应的右端点这段区间内往上往下走的最小值和算出来看看够不够边长就行了。

$O(nm+nk+mk)$。

Problem 6：$\texttt\color{red}CF850D$

给定一个竞赛图的出度集合 $S$，构造点数最小的图。

题解

题目给了你个定理，按照这个定理可以 dp 出点数。

然后你每次找到出度最大的点，让他赢出度最小的几个点，输给剩下的点，做 $n$ 轮这样就是对的。

Problem 7：$\texttt\color{green}CF30E$

给串 $S$，求把 $S$ 拆成 $xaybza'$ 使得 $aba'$ 是长度为奇数的回文串。最大化 $aba'$ 的长度。

题解

首先可以 manacher 枚举极长的 $b$。由于 $a'$ 是后缀，可以把 $S$ 对 $S$ 的反串跑 kmp 匹配，这样可以得到每个前缀的子串对应的最大后缀长度。

Problem 8：$\texttt\color{green}CF1697F$

题意：构造 $a$ 不降，值域 $k$，满足若干条件。

条件形如 $a_i\neq x$ 或 $a_i+a_j\ge x$ 或 $a_i+a_j\le x$。

$k\le 10$。

题解

2-sat，考虑 $a_i\ge x$ 是否成立。

Problem 9：$\texttt\color{red}CF418D$：ds，咕

Problem 10：$\texttt\color{green}CF288E$

由 $4,7$ 构成的数是好数。现在给你两个 $n$ 位好数，把他们之间的好数从小到大记为 $a_1,\cdots,a_k$，求 $\sum\limits_{i=1}^{k-1}a_ia_{i+1}$。

题解

差分之后数位 dp，然后枚举 $a_i$ 最后 $\cdots 744444$ 有多少个 $4$，前面维护 $0$ 到 $2$ 次方和，这样可以 $O(n)$。

Problem 11：$\texttt\color{red}CF776F$

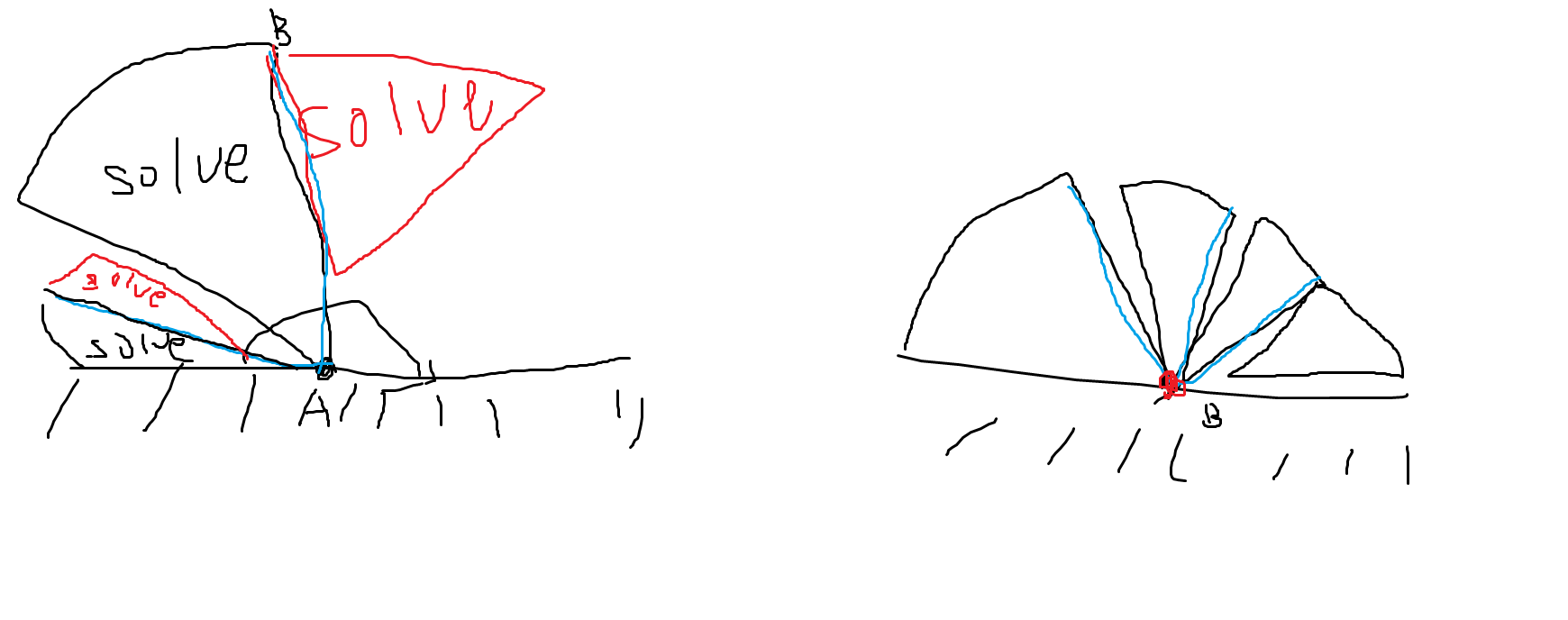
题意：$n$ 边形的顶点间连了若干不交线段，给每个区域定 $[1,20]$ 的值使得两个同值区域中间必须通过至少一个值更小的区间才能走通。

题解

显然这个东西叫做点分治。

Problem 12：$\texttt\color{green}CF1290D$（交互）

题意：

一个长度最大为 $k$ 的队列 $Q$ 初始为空。一个未知序列 $a$ 长度为 $n$。

两种操作：

$? x$，查询队列中是否有和 $a_x$ 相同的元素，然后把 $a_x$ 加入队列。如果超长度就从另一端 pop。

$r$，清空队列。

$1.5\frac{n^2}k$ 次询问，$30000$ 次清空内求出 $a$ 有多少不同的数。

$n,k$ 是 $2$ 的幂。

题解

考虑对于每个 $i$，如果不存在 $j\lt i$ 和他相同就计入答案。

分块，$0.5k$ 个数放一块里面，然后我们对于每个编号 $i\lt j$ 的块，先把 $i$ 丢进去再把 $j$ 丢进去就可以更新块 $j$ 的答案。

这样太浪费了。考虑先枚举步长 $gap$，然后枚举 $x\le gap$，依次把 $x,x+gap,x+2gap\cdots$ 这样加进去，询问次数就是 $1.5\frac{n^2}{k}-0.5n$。

Problem 13：$\texttt\color{red}CF204E$（string）：咕。

Problem 14：$\texttt\color{red}CF1172D$（构造）

题意：

在 $n\times n$ 的棋盘上放若干对传送门（多传送门不能放同一个位置），棋子走到传送门的一端会被传送到另一端。

给定你棋子从每一列棋盘上边界一直往下走，和每一行棋盘左边界往右走，会在哪个位置走出棋盘。构造一组传送门方案。

题解

大概做法是，每次只在最左边和最上边放传送门，把要到最左边和最上面一列的目标传送过去，转换成 $(n-1)\times (n-1)$ 的情况。这样就能做了。

Problem 15：$\texttt\color{green}CF79E$（构造）

题意：

$n\times n$ 的棋盘，一个边长 $c$ 的子矩阵里面每个位置有个血量 $t$ 的 bot。你要从 $(1,1)$ 走到 $(n,n)$，向右或者向下。你每走一步每个 bot 的血量会减少它到你的哈密顿距离。你不能让 bot 的血量小于 $0$。找到字典序最小的方案。

?

为什么我做法是对的啊？

Problem 16：$\texttt\color{red}CF933D$

题意：记 $f(i)$ 表示半径 $i^2$ 的圆内（包括边界）的整点数，$g(n)=\sum\limits_{i=1}^nif(i)$，求 $\sum\limits_{i=1}^ng(i)$。

$n\le 10^{12}$。

题解

考虑先只计算一个象限的答案。枚举 $x$ 坐标，$y$ 的贡献是一个多项式，然后就可以插值了。

Problem 17：$\texttt\color{red}CF1372E$

题意：$n\times m$ 的矩形，每行被分成了若干 $1\times x$ 的矩形。现在每行的每个矩形里面放一个 $1$，最大化每列和的平方之和。

$n,m\le 100$。

题解

对列区间 dp，一个区间的策略一定是：选择一列 $k$，找出所有完全在区间内，且跨 $k$ 的矩形，全都放在 $k$ 这一列。随便 dp 就能 $O(n^3)$ 或者 $O(n^4)$。

Problem 18：$\texttt\color{green}CF241D$

题意：给定长度 $n$ 的排列和一个质数 $p$，找到一个子序列，$\operatorname{xor}=0$，拼接起来得到的数 $\bmod p=0$。

$n,m\le 50000$。

题解

只取值 $\le 24$ 的位置爆搜就行了。考虑如果 $p$ 是 $2$ 或者 $5$ 显然可行。否则可以假装每个子集取模之后是随机的，一共有 $524287$ 组搜出来满足异或条件的。错误率非常低。

Problem 19：$\texttt\color{red}CF1342F$

题意：长度 $n$ 序列，每次选择两个数，删除一个加到另一个上面，求最少几次操作递增。

$n\le 15$。

题解

可以把题目理解成分成尽量多个子集，集合的和递增，且可以在每个集合选一个代表位置也递增。

$dp_{i,pos,S}$ 表示选了 $i$ 个集合，第 $i$ 个的代表位置是 $pos$，已经用掉了 $S$ 集合里的数。转移简单的。$O(3^nn^2)$。

Problem 20：$\texttt\color{red}CF1070M$

题意：平面上 $n$ 黑点 $m$ 红点，你要连一个树：边不能相交；同色点不能连边；第 $i$ 个红点度数 $r_i$。

$n,m\le 3000$。

题解

考虑当前处理集合 $V$。

每次找到 $V$ 最下面的点讨论。其他点先极角排序。

如果是黑点，每次扫找到一个除了最右边红点，内部能处理完的区间，和右端点的红点连一条边，递归；完了之后还需要把这个红点处理完，所以继续往右边扫一个恰好内部处理完区间然后递归。

如果是红点，每次扫一个内部处理完的区间，连右边的黑点然后递归。如果最后一个区间处理不完就往前面塞一个点递归处理，就这样：